Fibonacci sequences appear in biological settings,^[9] in two consecutive Fibonacci numbers, such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple,^[10] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone,^[11] and the family tree of honeybees.^[58] However, numerous poorly substantiated claims of Fibonacci numbers or golden sections in nature are found in popular sources, e.g., relating to the breeding of rabbits in Fibonacci's own unrealistic example, the seeds on a sunflower, the spirals of shells, and the curve of waves.^[59]rk! 

 this expression can be used to decompose higher powers as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of and 1. The resulting recurrence relationships yield Fibonacci numbers as the linear coefficients: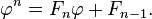 

This equation can be proved by induction on n. This expression is also true for n < 1 if the Fibonacci sequence F_n is extended to negative integers using the Fibonacci rule